Problem Hetmanów

Na stronach tych omówione są najciekawsze algorytmy omawiane na wykładzie ze Wstępu do Informatyki na pierwszym roku studiów informatycznych na Wydziale PPT Pwr.

☰ Menu

Brak

nikt

Problem hetmanów

Hetman jest figurą szachową, która bije figury znajdujące się w tej samej kolumnie, wierszu lub przekątnej, co on sam. W jaki sposób rozstawić osiem hetmanów na tradycyjnej szachownicy 8x8 tak, aby wzajemnie się nie atakowały? Ile jest możliwych rozstawień?

Historia problemu

Jest to problem szachowy i matematyczny, sformułowany w połowie XIX w. przez Maksa Bezzela i Franza Naucka. Dotyczy on takiego rozmieszczenia 8 hetmanów na szachownicy o wymiarach 8x8, aby żadne dwie figury nie szachowały się wzajemnie, czyli aby nie znajdowały się w tym samym wierszu, kolumnie, czy ukośnym rzędzie. Początkowo rozważano zwykłą szachownicę, ale z czasem rozszerzono problem na dowolną (kwadratową) szachownicę.

Sformułowanie analityczne problemu

Niech (i,j) (m,n) będą współrzędnymi dwóch hetmanów

dwa hetmany stoją na jednej linii wtedy i tylko wtedy gdy i=m lub j=n
dwa hetmany stoją na jednej diagonali wtedy i tylko wtedy gdy i=m±x i j=n±x

gdzie wartość x jest niezależna w obu równaniach. Jak można stwierdzić całkowita ilość rozwiązań nie może przekroczyć 8!=40320.

Algorytm z powrotami

Stawiamy hetmana w pierwszym wierszu w pierwszej kolumnie. Przechodzimy do drugiego wiersza i szukamy pierwszej, wolnej kolumny - w tym wypadku będzie to kolumna trzecia (1. kolumna jest zajęta ze względu na to, iż w pierwszym wierszu już stoi na niej hetman, a 2. gdyż hetman z pierwszego wiersza "patrzy" na nią po przekątnej). Ilustruje to poniższy diagram:

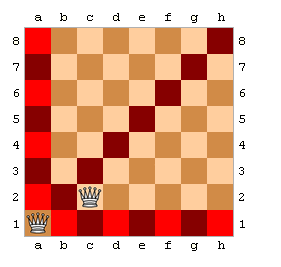
Podobnie postępujemy z kolejnymi wierszami. W momencie, gdy któregoś hetmana nie da się postawić, (w każdej z 8 kolumn hetman będzie atakowany) to cofamy się o jeden wiersz i przesuwanmy hetmana na kolejne wolne pole. Jeśli takie nie istnieje, to znowu się cofamy itd. Ta cecha sprawia, że algorytm ustawiający hetmany na szachownicy jest przykładem rekurencji z powrotami. Gdy udało się szczęśliwie postawić 8. hetmana oznacza to, że znaleźliśmy rozwiązanie (zapisujemy ustawienia wszystkich hetmnanów np. w pliku wynikowym). Jeśli okaże się, że hetmana z pierwszego wiersza nie ma już gdzie postawić, to znaczy, że wszystkie możliwe kombinacje zostały już sprawdzone.

Algorytm w języku C

const int n = 8; int y_position[n]; int counter = 1; bool is_free(int x, int y) { for (int i=0; i<x; i++) { if (y == y_position[i] || abs(x-i) == abs(y_position[i])) return false; } return true; } void hetman(column) { for (int i=0; i<n; i++) { if (is_free(column, i)) { y_position[kol]=i; if (column == n-1) { print(); counter++; return; } hetman(column+1); } } } hetman(0);

Algorytm w języku JavaScript

var n = 8; var yPosition = []; var counter = 1; function isFree(x, y) { for (var i=0; i<x; i++) { if (y == yPosition[i] || Math.abs(x-i) == Math.abs(y-yPosition[i])) return false; } return true; }; function hetman(column) { for (var i=0; i<n; i++) { if (isFree(column, i)) { yPosition[column] = i; if (column == n-1) { print(); counter++; return; } hetman(column+1); } } }; hetman(0);

Wszystkie kombinacje

Kolejne wyrazy ciągów reprezentują indeks hetmana w kolejnych wierszach planszy, są to wszystkie kombinacje.

Po wciśnięciu przycisku zostanie pobrane rozwiązanie z listy powyżej i na jego podstawie wygeneruje się plansza z ustawieniem hetmanów, spełniającym problem. Kolejne kliknięcie przejdą po kolejnych rozwiązaniach.